DECIMALES
Simetrias
TEMA 12: LONGITUD,CAPACIDAD,MASA Y SUPERFICIE.
SISTEMA MÉTRICO DECIMAL
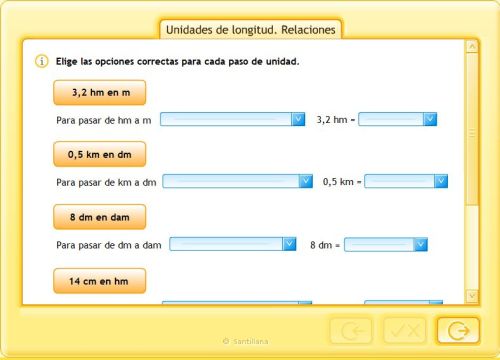
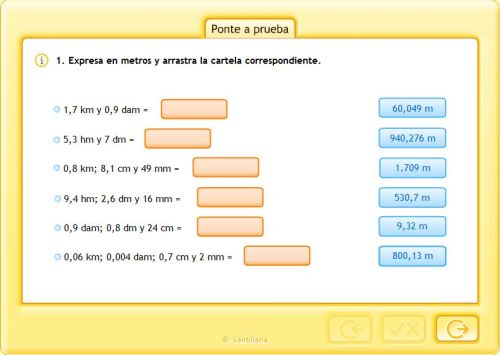
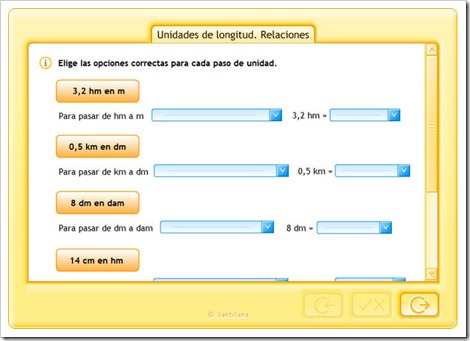
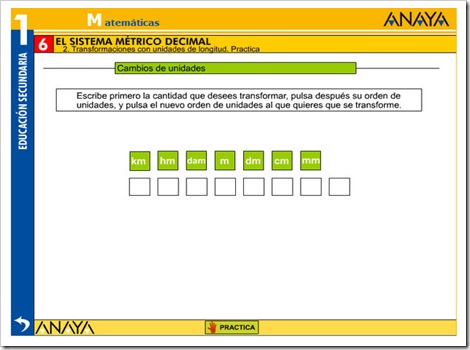
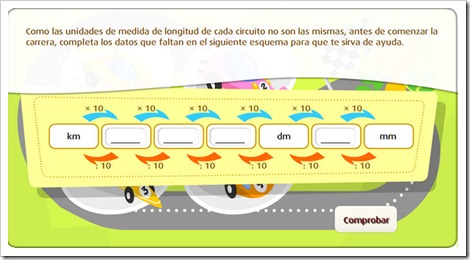
UNIDADES DE LONGITUD. RELACIONES.
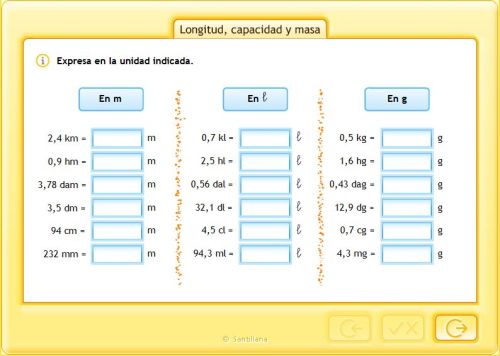
APRÉNDELO TÚ MISMO/A
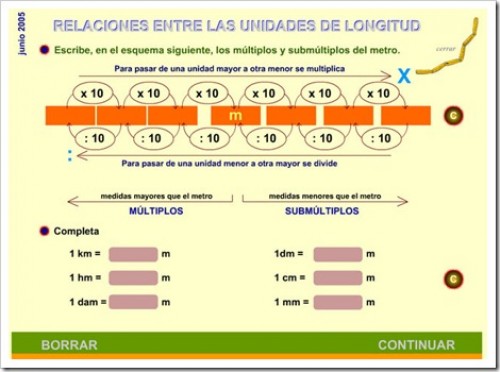
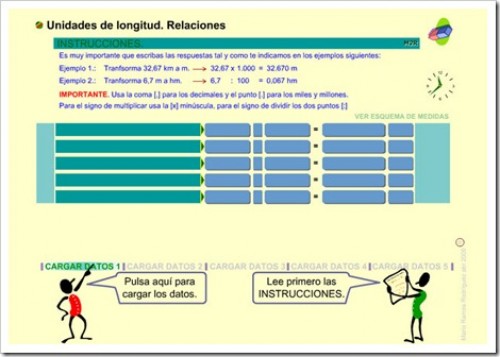
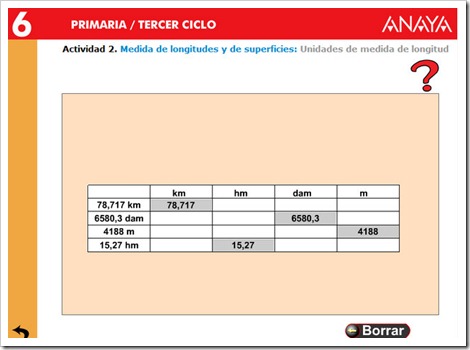
UNIDADES DE LONGITUD
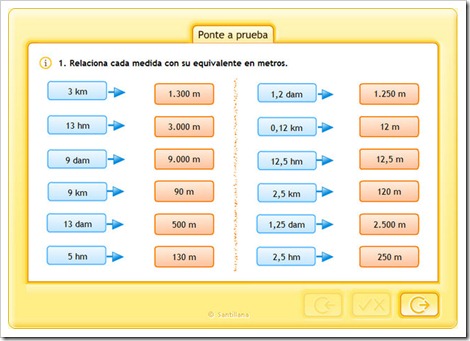
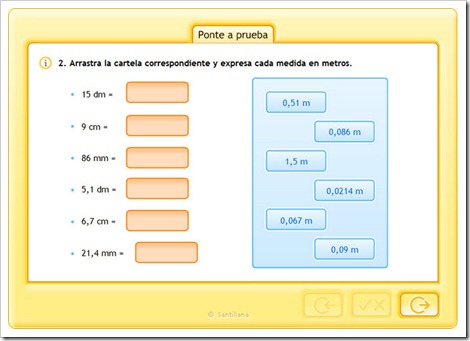
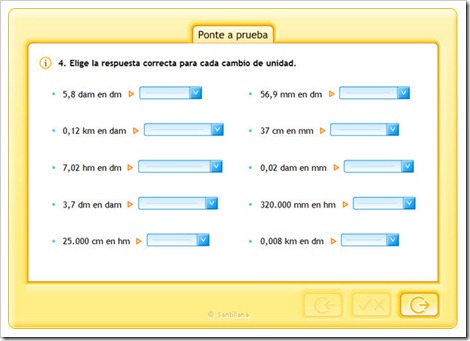
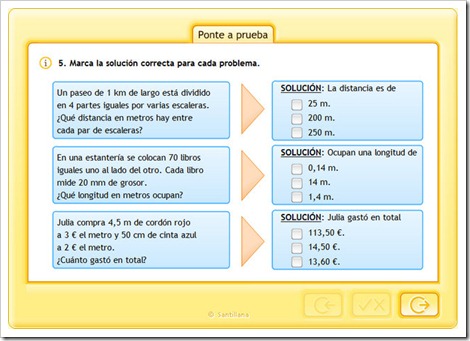
COMPRUEBA LO QUE SABES HACIENDO EL SIGUIENTE TEST.
www2.gobiernodecanarias.org
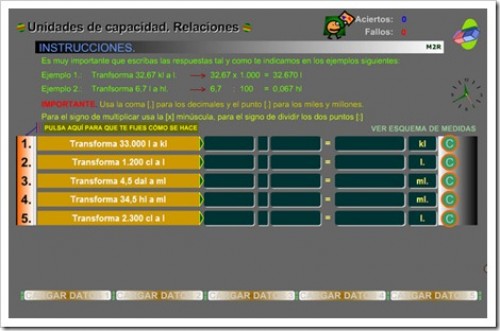
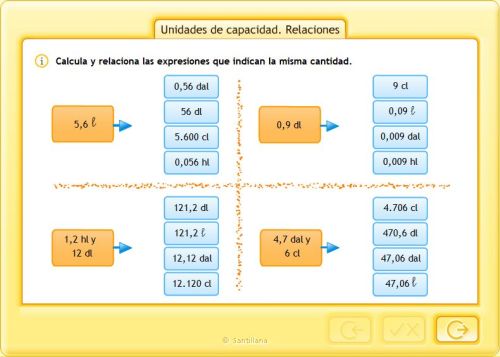
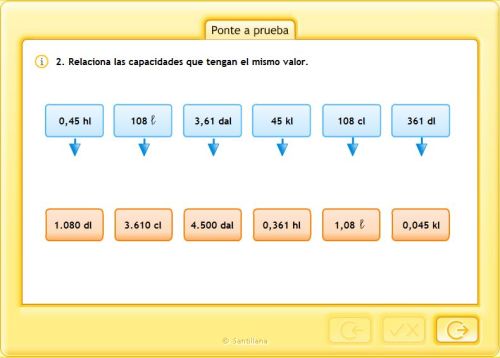
UNIDADES DE CAPACIDAD. RELACIONES
www2.gobiernodecanarias.org
EL PESO Y LA MASA
TEORÍA
ntic.educacion.es
ntic.educacion.es
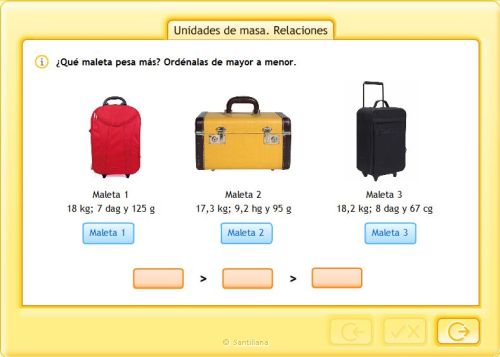
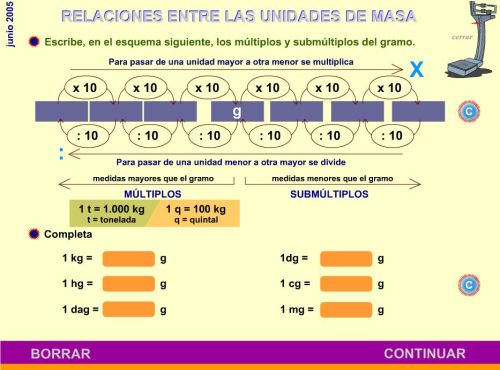
UNIDAD DE MASA. RELACIONES
www2.gobiernodecanarias.org
/www2.gobiernodecanarias.org
www2.gobiernodecanarias.org
UNIDADES DE SUPERFICIE
www3.gobiernodecanarias.org
DENSIDAD DE POBLACIÓN
UNIDADES AGRARIAS
OPERACIONES CON MAGNITUDES
ntic.educacion.es
ntic.educacion.es
/ntic.educacion.es
ntic.educacion.es
AUTOEVALUACIONES
-
AUTOEVALUACIÓN 1. LA LONGITUD
-
AUTOEVALUACIÓN 2. LA CAPACIDAD
-
AUTOEVALUACIÓN. 3. LA MASA. PESO.
-
AUTOEVALUACIÓN 4. MEDIDAS DE SUPERFICIE.
MÁS RECURSOS
Recopilación hecha por el C.E.I.P. “Ntra. Sra. de Loreto” – Dos Torres (Córdoba)
sUnidad 12: Longitud, capacidad, masa y superficie
|
Web interactivas
|
Jclic
|
Unidades de longitud. Relaciones
|
||
Unidades de capacidad. Relaciones
|
||
Unidades de masa. Relaciones
|
||
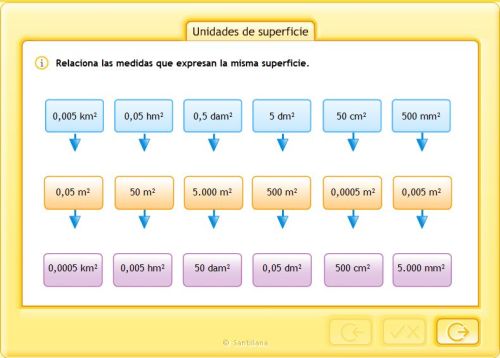
Unidades de superficie
|
||
|
(SM Ud. 9)
|
||
|
(SM Ud. 9)
|
||
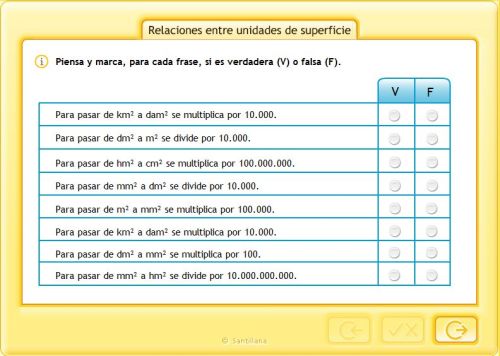
Relaciones entre unidades de superficie
|
||
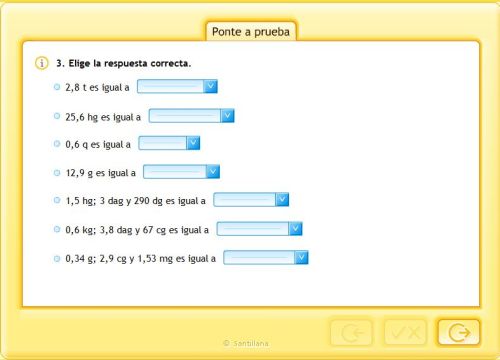
Unidades agrarias
|
||
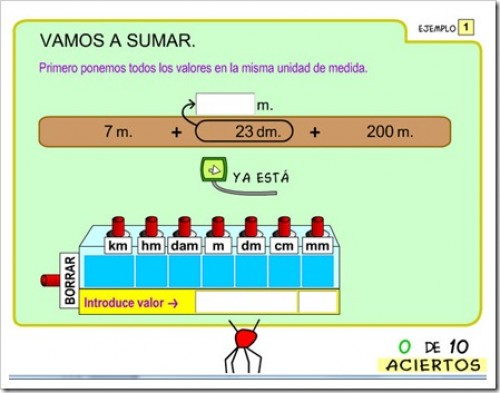
Sumar un número decimal y un natural
|
||
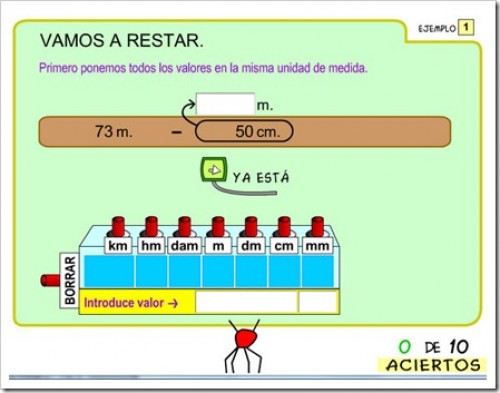
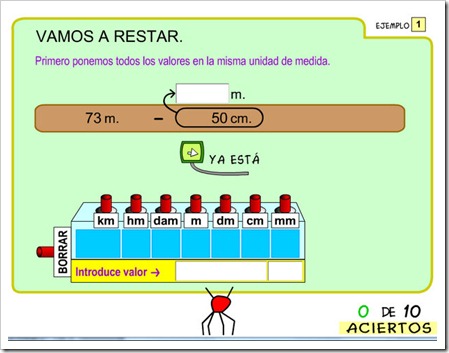
Restar un número natural a un decimal
|
||
P: Representar gráficamente la situación
|
||
|
(SM Ud. 9)
|
PROBABILIDAD
Unidad 15: Estadística
|
Web interactivas
|
Jclic
|
Variables estadísticas
| ||
|
(SM Ud. 15)
| ||
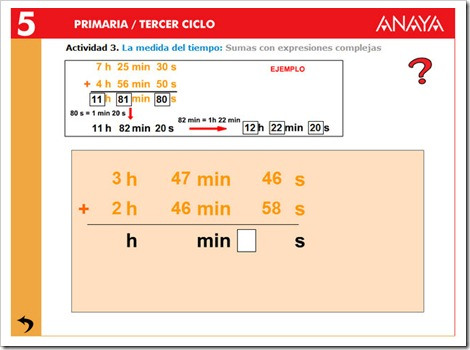
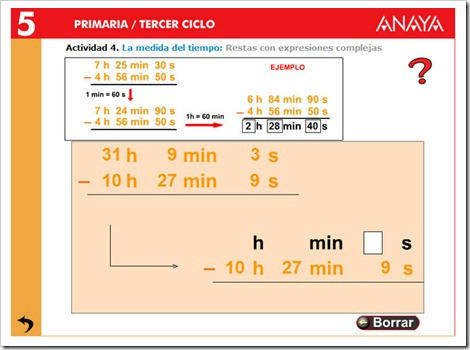
14.El tiempo y el dinero
SUDOKUS PARA NIÑOS
¿Cómo se hace un Sudoku?
El Sudoku estándar (porque hay múltiples variantes)
presenta una cuadrícula de 81 casillas, de de 9 filas x 9 columnas,
compuesta por 9 bloques de 3 filas × 3 columnas, que también se llaman
“cajas”.
Al inicio del sudoku vemos que algunas casillas ya contienen números. Estos números iniciales son conocidos como "números dados" (también hay quien los denomina "pistas").
Nuestro objetivo es rellenar las casillas vacías con números del 1 al 9. Pero estos números tenemos que colocarlos de tal forma que cada columna, cada fila y cada bloque sólo puede contener los números del 1 al 9 SÓLO UNA VEZ.
Al inicio del sudoku vemos que algunas casillas ya contienen números. Estos números iniciales son conocidos como "números dados" (también hay quien los denomina "pistas").
Nuestro objetivo es rellenar las casillas vacías con números del 1 al 9. Pero estos números tenemos que colocarlos de tal forma que cada columna, cada fila y cada bloque sólo puede contener los números del 1 al 9 SÓLO UNA VEZ.
Así, el resultado es que cada número aparece
únicamente una vez en cada una de las tres "direcciones". De ahí su
nombre: “Su” = número; “Doku” = único".
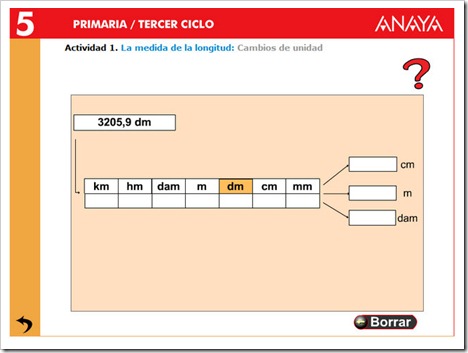
Aprende las Medidas de Longitud
Las medidas de longitud se emplean para medir la distancia existente entre dos puntos. La unidad básica es el metro.
En la siguiente tabla de posición se muestran el nombre, la abreviatura y el valor de los múltiplos (km,hm,dam) y submúltiplos (dm, cm, mm) más usuales delmetro. En algunos libros de Matemáticas el hectómetro se abrevia como Hm y el decámetro como Dm.
kilómetro hectómetro decámetro metro decímetro centímetro milímetro km hm dam m dm cm mm 1.000 m 100 m 10 m 1 m 0,1 m 0,01 m 0,001 m
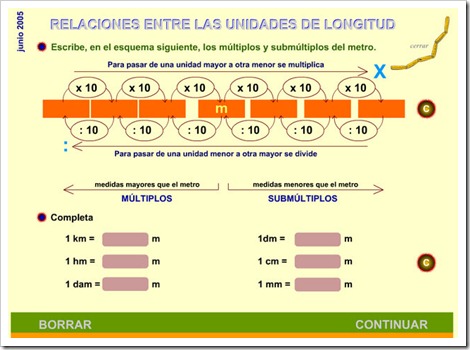
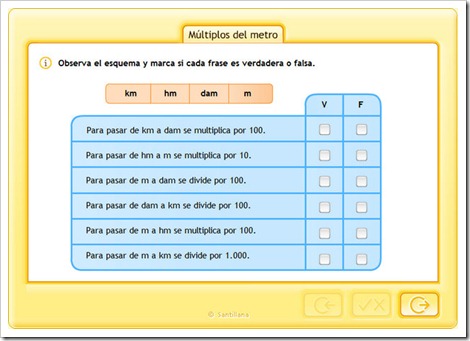
Como puede observarse en la tabla, el valor de cada unidad es 10 veces mayor que el de su derecha. Es decir:
1 km = 10 hm = 100 dam = 1.000 m = 10.000 dm = 100.000 cm = 1.000.000 mm
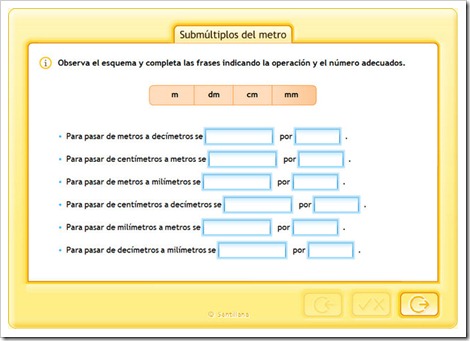
Para convertir una unidad determinada en otra pedida, situada a su derecha(menor), tenemos que multiplicarla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida.
Recuerda que multiplicar por la unidad seguida de ceros equivale a "correr la comade los decimales" hacia la derecha tantos lugares como ceros acompañan a la unidad.
Ejemplo: Convertir 9 km en m.
Como desde km a m hay 3 posiciones, hacia la derecha, tendremos que multiplicarpor 1.000. Por lo tanto, 9 km = 9 x 1.000 = 9.000 m.
Lo que equivale a correr la coma 3 lugares a la derecha: 9,0000 X 1.000 = 9.000,0
(Los ceros a la derecha de la coma de decimales no tienen valor y podemos poner los que necesitemos)
Para convertir una unidad determinada en otra pedida, situada a su izquierda(mayor), tenemos que dividirla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida.
Recuerda que dividir por la unidad seguida de ceros equivale a "correr la coma de los decimales" hacia la izquierda tantos lugares como ceros acompañan a la unidad.
Ejemplo: Convertir 120 mm en dam.
Como desde mm a dam hay 4 posiciones, hacia la izquierda, tendremos que dividirpor 10.000. Por lo tanto, 120 mm = 120 : 10.000 = 0,012 dam.
Lo que equivale a correr la coma 4 lugares a la izquierda: 00120,0 : 10.000 = 0,012.
(Los ceros a la izquierda de un número entero no tienen valor y podemos poner los que necesitemos)
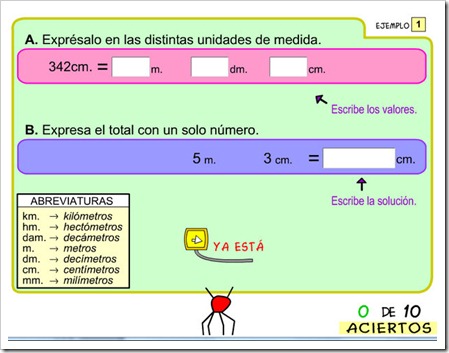
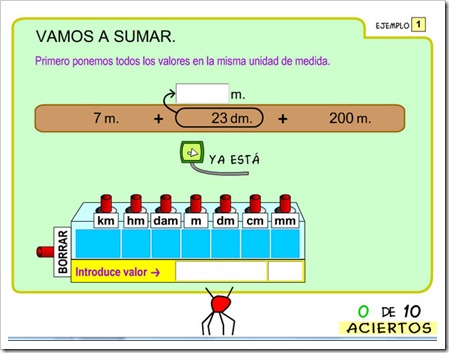
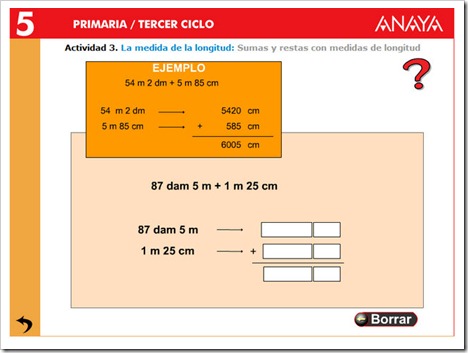
Si queremos convertir una cantidad compleja (que contiene unidades distintas) en otra pedida, lo primero que haremos será convertir cada una de las unidades a la unidad pedida y después, cuando estén todas en la unidad pedida, las sumamos.
Ejemplo: Convertir 2 km, 15 m, 350 dm en dam.
1º De km a dam hay 2 lugares a la derecha, multiplicaremos por 100,
2 x 100 = 200 dam.
2º De m a dam hay 1 lugar a la izquierda, dividiremos por 10,
15 : 10 = 1,5 dam.
3º De cm a dam hay 3 lugares a la izquierda, dividiremos por 1.000,
350 : 1.000 = 0,35 dam.
4º Por último, sumamos los decámetro y nos queda:
200 dam + 1,5 dam + 0,35 dam = 201,85 dam
El resultado es: 2 km, 15 m, 350 dm = 201,85 dam.
Hay otras medidas de longitud, que no emplearemos en los juegos, por ejemplo:
Miriámetro (mam) que equivale a 10.000 metros.
Año-luz, para medir grandes distancias (la que recorrería la luz en un año solar) que equivale a 9.461.000.000.000 metros.
Micra, para medir distancias microscópicas, que equivale a una millonésima parte del metro (0,000001 m).
| kilómetro | hectómetro | decámetro | metro | decímetro | centímetro | milímetro |
| km | hm | dam | m | dm | cm | mm |
| 1.000 m | 100 m | 10 m | 1 m | 0,1 m | 0,01 m | 0,001 m |
Como puede observarse en la tabla, el valor de cada unidad es 10 veces mayor que el de su derecha. Es decir:
Lo que equivale a correr la coma 3 lugares a la derecha: 9,0000 X 1.000 = 9.000,0
(Los ceros a la derecha de la coma de decimales no tienen valor y podemos poner los que necesitemos)
Lo que equivale a correr la coma 4 lugares a la izquierda: 00120,0 : 10.000 = 0,012.
(Los ceros a la izquierda de un número entero no tienen valor y podemos poner los que necesitemos)
2 x 100 = 200 dam.
2º De m a dam hay 1 lugar a la izquierda, dividiremos por 10,
15 : 10 = 1,5 dam.
3º De cm a dam hay 3 lugares a la izquierda, dividiremos por 1.000,
350 : 1.000 = 0,35 dam.
4º Por último, sumamos los decámetro y nos queda:
200 dam + 1,5 dam + 0,35 dam = 201,85 dam
El resultado es: 2 km, 15 m, 350 dm = 201,85 dam.
Año-luz, para medir grandes distancias (la que recorrería la luz en un año solar) que equivale a 9.461.000.000.000 metros.
Micra, para medir distancias microscópicas, que equivale a una millonésima parte del metro (0,000001 m).
11.Unidades de longitud
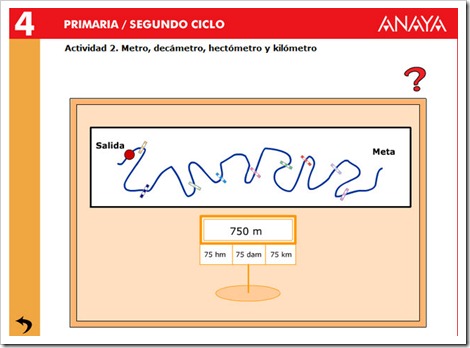
Aprendemos medidas de longitud jugando
Enlace a la página de ntic.educación y a la aplicación de Marisa Carrillo, Enrique Hernán y Laura Hernán para aprender y jugar con las medidas de longitud
Enlace a la página de ntic.educación y a la aplicación de Marisa Carrillo, Enrique Hernán y Laura Hernán para aprender y jugar con las medidas de longitud
Tendremos que ir contestando preguntas con el metro, decímetro y centímetro para seguir nuestro camino
TODO SOBRE DECIMALES
LOS NÚMEROS DECIMALES
DESCOMPOSICIÓ DE NÚMEROSDECIMALS
LOS NÚMEROS DECIMALES
DESCOMPOSICIÓ DE NÚMEROSDECIMALS
CALCULANT PERCENTATGES (%) AMB REGLA DE TRES SIMPLE
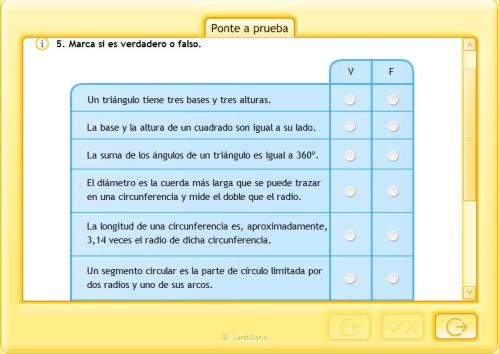
LA CIRCUNFERENCIA Y EL CÍRCULO
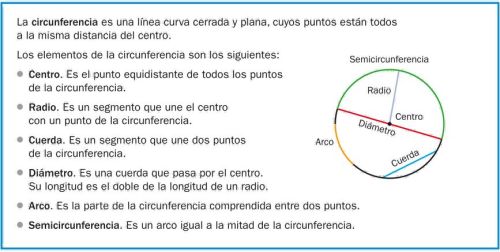
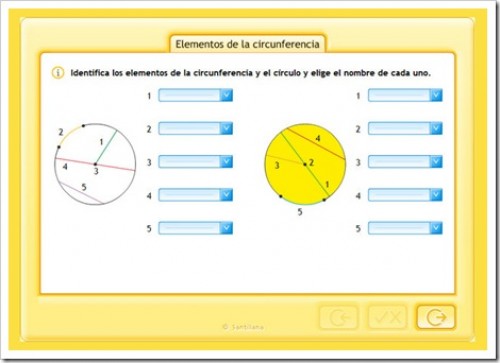
LA CIRCUNFERENCIA. ELEMENTOS
FÍJATE EN LA SIGUIENTE IMAGEN Y APRENDE LOS ELEMENTOS DE LA CIRCUNFERENCIA.
PRACTICA CON ESTAS ACTIVIDADES PARA QUE NO TE OLVIDES DE LO QUE HAS APRENDIDO.
ACTIVIDAD 1.
/www.e-vocacion.es
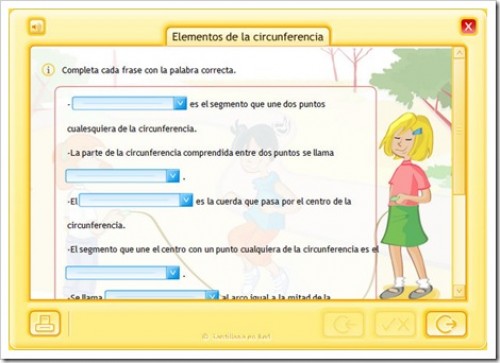
ACTIVIDAD 2.
http://www.e-vocacion.es
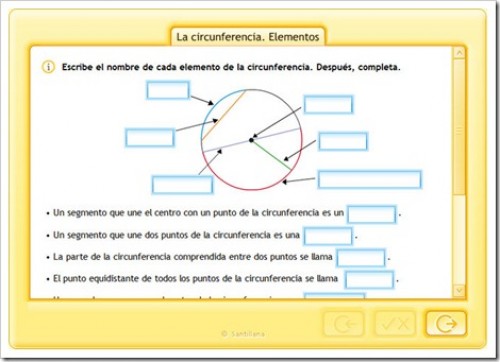
ACTIVIDAD 3
contenidos.santillanaenred.com
ACTIVIDAD 4
/www.e-vocacion.es
LONGITUD DE LA CIRCUNFERENCIA
E-VOCACIÓN
/www.genmagic.net
PINCHA PRIMERO EN LA ZONA DE:
“PARA APRENDER” Y DESPUÉS, ¡PRACTICA!
AHORA ESTÁS PREPARADO/A PARA PRACTICAR
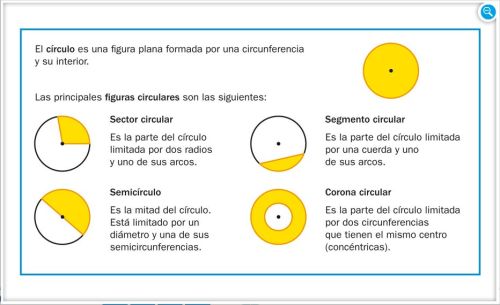
EL CÍRCULO Y LAS FIGURAS CIRCULARES
OTRO REPASITO
AHORA… PUEDES PRACTICAR.
REPASAMOS LA CIRCUNFERENCIA Y EL CÍRCULO CON ESTA ESTUPENDA PRESENTACIÓN
entra ahora en la sección de:
para practica.
comprueba lo que aprendiste.
POSICIONES RELATIVAS DE RECTAS Y CIRCUNFERENCIAS
FÍJATE EN LAS DISTINTAS POSICIONES Y APRÉNDELAS
RECTAS INTERIORES Y EXTERIORES
AHORA PODRÁS APRENDER CON UN JUEGO MUY ENTRETENIDO.
REPASO FINAL
¡A VER QUÉ PUNTUACIÓN SACAS! ¡ÁNIMO!
décimas, centt
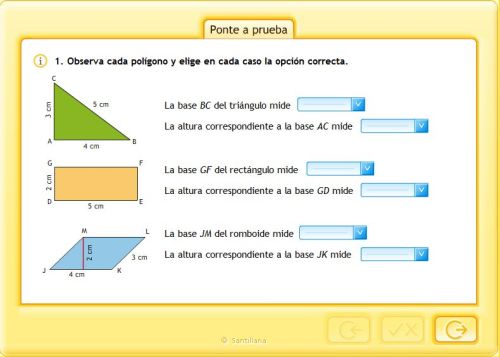
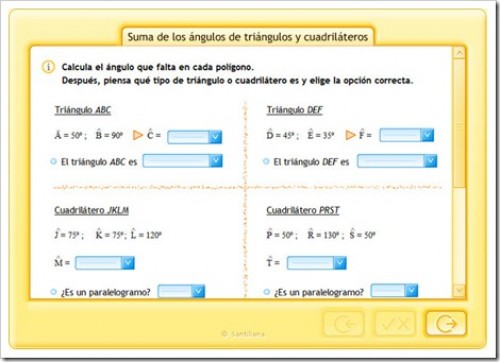
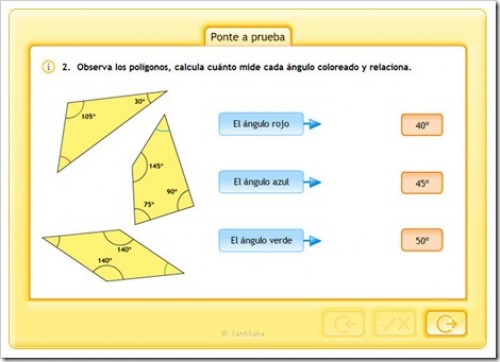
TRIÀNGULOS Y CUADRILATEROS 1
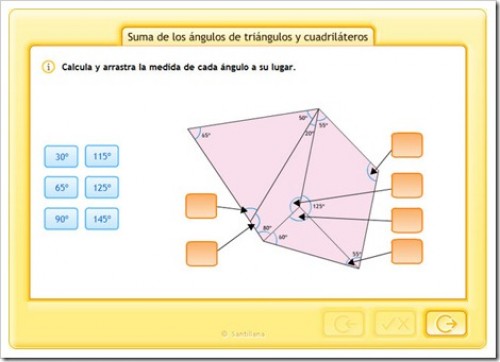
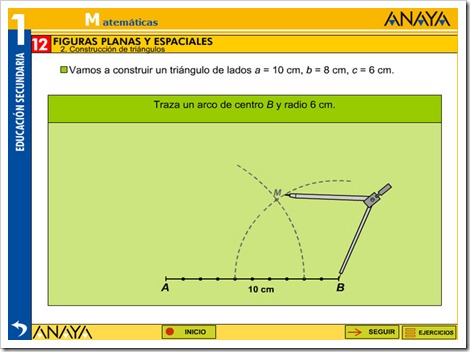
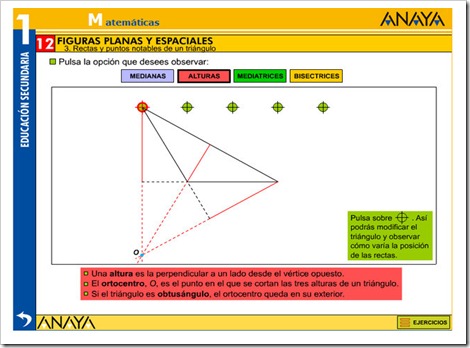
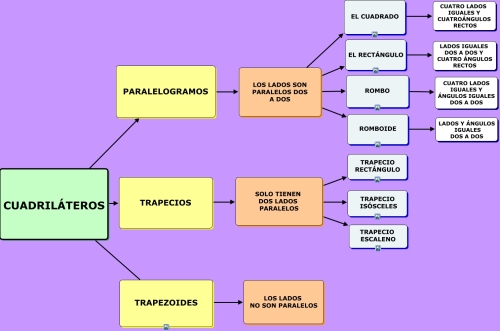
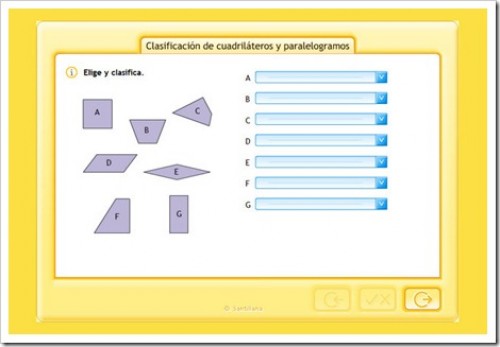
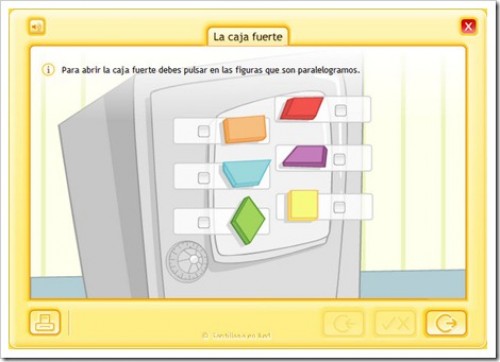
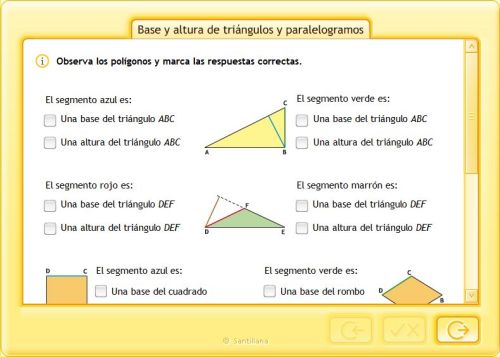
TRIÁNGULOS Y CUADRILATEROS
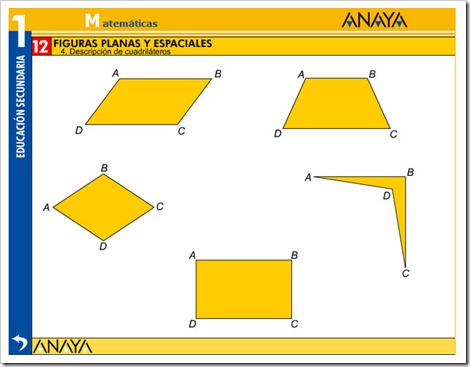
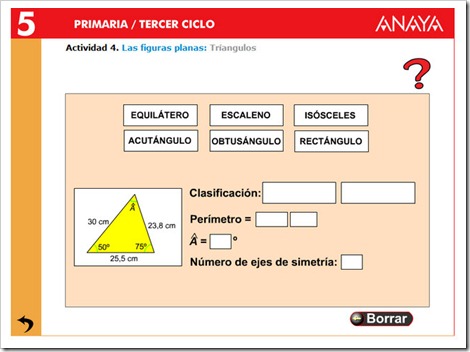
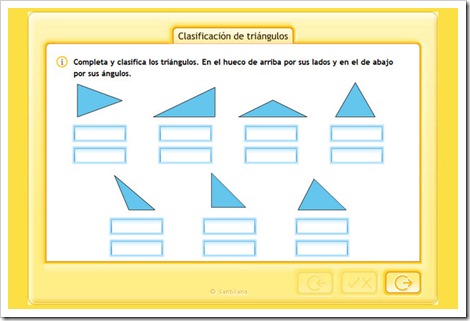
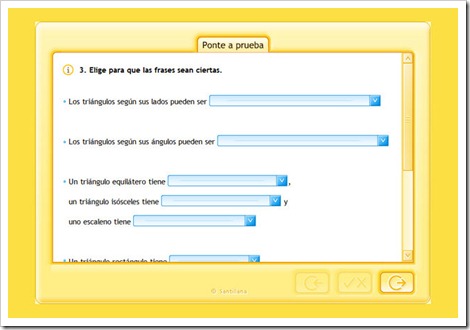
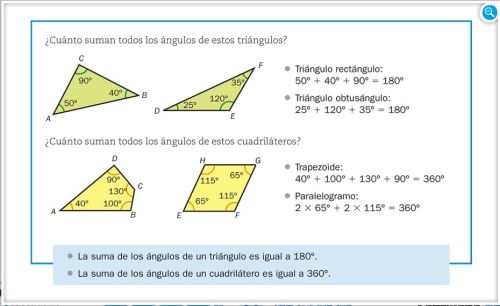
Pincha en la imagen para ampliar la imagen y podrás ver mejor la explicación.
ampliar la imagen y podrás ver mejor la explicación. 
fracciones 2
REPRESENTACIÓN DE FRACCIONES
SUMA Y RESTA DE FRACCIONES CON IGUAL DENOMINADOR
REPRESENTACIÓN DE FRACCIONES
SUMA Y RESTA DE FRACCIONES CON IGUAL DENOMINADOR
PROBLEMAS VARIADOS
MÁS RECURSOS DE MATEMÁTICAS
Ejercicios de Matemáticas
MULTIPLICACIÓN: PROPIEDAD ASOCIATIVA
editorialteide
Juego: Propiedad distributiva multiplicación
Juego sobre la propiedad distributiva de la multiplicación que me ha encantado.
¡Espero que a vosotros también!
¡Espero que a vosotros también!
LOS NÚMEROS ROMANOS
5.- Aprende a dividir; Aprende a dividir tú solo. Por una, dos y tres cifras.
| ||||
| 19.- Aprende a dividir tú sólo | 20.- Divide por una cifra | 21.- Divide por dos cifras | ||
Si te equivocas, el ordenador te corregirá los errores.
|
Introduce el número correcto y aprieta la tecla de entrada.
|
Introduce el número correcto y aprieta la tecla de entrada.
| ||
 | |  | ||
| 22.- Divide por tres cifra | 23.- La prueba del 9 | |||
Introduce el número correcto y aprieta la tecla de entrada.
|
Comprueba si has hecho bien tus divisiones.
| |||
 |  | |||
HISTORIA DE LA NUMERACION
Juego muy entretenido para practicar la multiplicación.Os lo recomiendo bien para jugar solo o en compañía.
NÚMEROS DE 7 CIFRAS
No hay comentarios:
Publicar un comentario